I took the opportunity to participate in research projects all through my undergraduate and graduate studies. Being both a mechanical engineer and an aerospace engineer I was able to work in both departments and in different areas. I found the research at Georgia Tech to be interesting and rewarding, and it contributed greatly to my engineering education.
The knowledge gained from one of these research projects later led to me writing my book Python Scripts for Abaqus - Learn by Example (external website: www.AbaqusPython.com)
You can read more about each of these research projects below: (click to locate on page)
- Effect of mesh topologies on Crack Propagation using Cohesive Elements
- Design and Optimization of Blast Resistant Panels
- Development of materials and structures for Morphing Wings
Effect of Mesh Topologies on Crack Propagation using Cohesive Elements
Institute: Daniel Guggenheim School of Aerospace Engineering, Georgia Tech
Advisor: Dr. Julian Rimoli
Team: The team consists of Dr Rimoli and I.
(I am currently working on this research - Spring 2012 - in partial fulfillment of my degree requirements)
Briefly (as stated on resume):
- Created an automated MATLAB script to examine a mesh, insert cohesive elements in suitable locations, create new coordinate and connectivity matrices, and generate a ready-to-run Abaqus input file with required material and section properties, loads/BCs and output requests
- Conducted studies to determine cohesive element properties for traction-separation behavior
- Simulating crack propagation with various mesh topologies and comparing results to experimental observations
- The research is being conducted at the request of Sandia National Laboratories
Details:
In finite element analysis, crack propagation is often modeled using cohesive elements. Cohesive elements are great for modeling situations/phenomena such as adhesives, delamination and fracture. The modeling strategy depends greatly on the type of effect being modeled. Crack propagation using cohesive elements is of interest to Sandia National for their research in nuclear energy, and this research is being conducted at their request.
Since we are interested in crack propagation, we are using cohesive elements with traction-separation behavior. Here we define the initial elasticity, the damage initiation, and the damage evolution in terms of energy dissipated for failure.
One of the problems with using cohesive elements for crack propagation is that the cohesive elements must lie along the crack path, or inversely, the crack propagates along a path defined by the cohesive elements. This means that mesh topology has a great impact on the path of the crack and can adversely affect the results. This creates a challenge in situations where it is necessary to accurately determine the direction of crack propagation without prior knowledge. The focus of the current research is to generate topologies which minimize this dependence.
We generate our meshes using in-house programs written in MATLAB which create the coordinate and connectivity matrices for the elements. These meshes are then imported into Abaqus. Inserting cohesive elements in the correct locations of an orphan mesh is nearly impossible in Abaqus/CAE (at least when there is no initial crack or it is very thin) hence I have written additional MATLAB scripts to accept a mesh, insert cohesive elements in the correct locations, and generate a complete input file (.inp) that can create the entire model (material properties, loads, bcs, steps etc) once imported into Abaqus.
We run numerous test cases for simple structures such as a plate with an edge crack where analytical solutions for stress intensity factor are available. An example of this is shown in the figure. The plate is fixed at the bottom, and a displacement boundary condition is applied at the top pulling it upward. An initial edge crack is present on the left edge of the plate although this is hard to see in the figure on the left. The figure on the right is the end result of the simulation, where the crack has traveled across the plate cutting it in half.

The animated gif image shows the edge crack propagating across the plate. (This mesh is quite coarse, finer meshes are used for most of our analyses).

In our traction separation model, the cohesive element damage profile is linear and is defined by the fracture energy. The following animation shows a few cohesive elements being damaged and subsequently removed from the view. The plot is of the field output variable SDEG which ranges from 0 (undamaged) to 1 (damaged).

The models are currently being applied to test cases where experiemtal results are available. Since this research is still in progress (and nothing has yet been published), I cannot post any further details/images at the moment..
Design and Optimization of Blast Resistant Panels
Institute: Systems Realization Laboratory, Woodruff School of Mechanical Engineering, Georgia Tech
Advisor: Dr. Janet Allen, Dr. Farrokh Mistree
Team: The team consisted of 2 professors/advisors, 2 PhD students focusing on design optimization studies, and me. My primary task was creating the finite element models, parameterizing them with Python scripts, and setting up a ModelCenter workflow to run the optimization studies.
Briefly (as stated on resume):
- Created computer models of honeycomb core sandwich structures and tested their response to high explosives using Abaqus/Explicit in order to find optimum structural and material configurations
- Compared theoretical predictions to numerical models previously generated by the lab
- Spent over 150 hours writing scripts for Abaqus in the Python programming language in order to automate simulations.
- Designed software interface in ModelCenter to run simulations and graph results.
- The research was conducted at the request of the Army Research Laboratory to produce blast resistant panels that can withstand landmine explosions.
- Published results
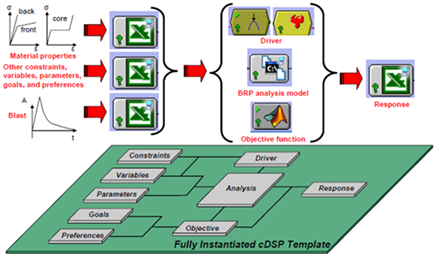
Details:
This work into blast resistant panels (BRPs) arose from a problem posed by the Army Research Laboratory through the participation of the Georgia Tech’s Systems Realization Laboratory in the Penn State – Georgia Tech I/UCRC for Computational Materials Design. There were a few different goals here.
- Design and efficiently analyze different BRP configurations
- Design a BRP concurrently with the material and design process
The first goal is self explanatory, and this was a primary task in this research. The second goal originated from a study of how to manage complexities in a design process - such as the integration of product design and material design - by a student on the team pursuing his PhD in Optimization studies. Design embodiment is the design phase which takes a product from the conceptual stage to the detail design stage. The design and analysis of the BRP was considered a good example for such a study on making design decisions.
Our work culminated in a paper "Designing Embodiment Design Processes for Blast Resistant Panels" which is available here.
Blast resistant panels are specially designed structures that can dissipate the forces generated by an explosion by plastic deformation.They absorb large amounts of energy through core crushing. They deflect less under the same impulse loading than a solid plate of equal mass. They are thus used as protective armor on military vehicles such as on the underside of a tank, to offer protection from landmines.
High explosives on detonation spontaneously release large amounts of heat and cause large changes in pressure due to the high rate of energy release. Explosive force is released in a direction perpendicular to the surface of the explosive. The impacting forces are expected to be unevenly distributed over the surface, and vary depending on the radial distance of each point on the surface of the BRP from the explosive. In addition, it is necessary to consider the fact that the impact of the blast will not be felt over the entire BRP surface at the same time. Abaqus/Explicit was used to perform the analysis.
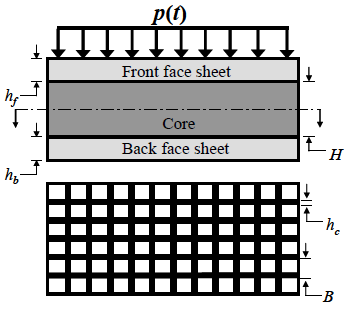
The BRP design used was that of a sandwich structure, consisting of two flat outer plates with a square honeycomb structure in the middle.
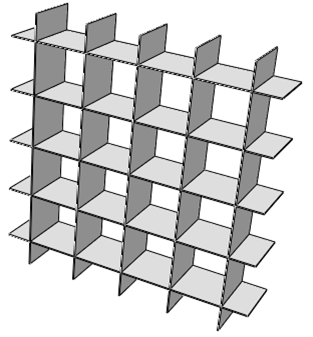
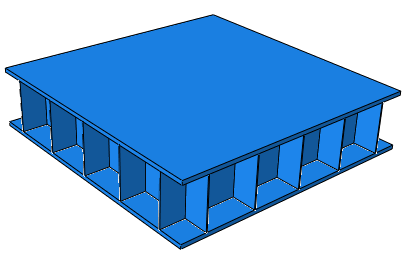
Only 1/4 of the BRP was modeled taking advantage of symmetry conditions to save on computational cost. Abaqus/Explicit was used for the analysis to account for the intertial effects of the impulsive explosion load. The core crushing is evident from the following figures.

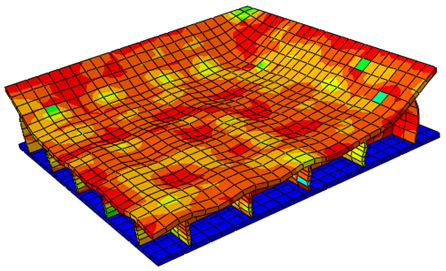
Since the study involved changing the dinensions and material properties of the above model, a fully parameterized Python script was written to automate the task in Abaqus. This script created the geometry based on dimensions provided as input variables. It then assembled the parts, applied the loads and boundary conditions, and ran the analysis, all without any further user intervention.
The script was then linked to ModelCenter from which the variables could be changed and the script initiated. The material plasticity data and teh load amplitude vs time data were stored in separate spreadsheets, and wrappers were created to extract this data from these spreadsheets and introduce them into the script. The Python script was also modified to perform post processing tasks and export relevant information to a results spreadsheet.
The ModelCenter workflow setup is displayed in the following figures.
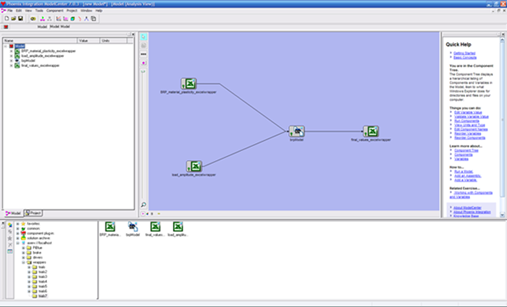
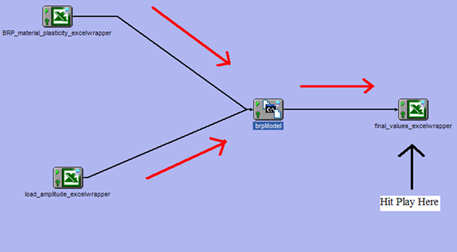
This model was then integrated into the embodiment design study which was later published.
After this research was completed and the results published, I began work on my book Python Scripts for Abaqus - Learn by Example (external website: www.AbaqusPython.com)
Development of materials and structures for Morphing Wings
Institute: School of Polymer, Textile and Fiber Engineering (now merged with School of Material Science and Engineering), Georgia Tech
Advisor: Dr. David Bucknall
Team: The team consisted of Dr. Bucknall and I.
Briefly (as stated on resume):
- Primary goal of research was to develop structural materials for use in morphing airplane wings, secondary goal was to develop foam-cell models to predict behavior
- Created foams coated with various thermally reactive polymers of different molecular weights and mechanically tested them (tensile, compression and dynamic mechanical analysis)
- Modeled foam cells in SolidWorks and simulated loading with FEA add-on CosmosWorks.
- Measured and analyzed polymer layers using optical and electron microscopes. Edited and extracted information from images using ImagePro and Adobe Photoshop
- I was awarded the Presidents Undergraduate Research Award (PURA) to fund this research
Details:
The purpose of the research was to create foam and polymer based materials and structures to be used in dynamically morphing airplane wings. The aims were to develop or use foams in combination with polymers and resins, to create materials and mechanical devices that change shape and retain this new shape in a consistent manner.
A couple of different strategies were considered.
The first one was that of a jointed cell like structure. This structure was a closed frame of plates of carbon fiber coated with resin (forming a composite) joined together with an elastomer. The carbon fibres composite plates formed a hard supporting material whereas the connective elastomeric bits formed the joints.
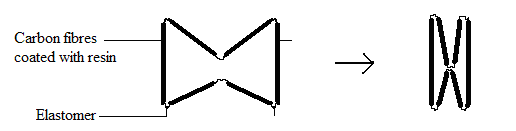
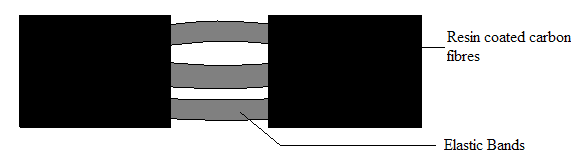
Experiments were conducted in the lab to find the optimum resin + hardener mix ratio and curing temperature and time. A resin HTR-212 and a hardener HT-360 were used with segments of carbon fiber. A vacuum oven was used for curing to study/prevent oxidation and bubble formation.
For initial testing purposes a single jointed structure with two composite plates was created.
Since the elastomers were embedded inside the composite plates, the curing operation took place with the elastomers in place. The following apparatus was developed.
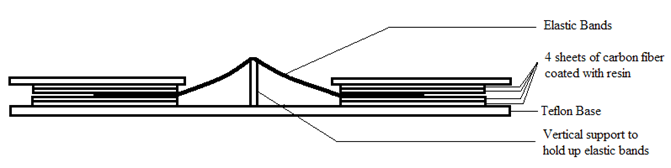
As the research proceeded, more complex arrangements were expermented with. Special molds had to be created for these. CAD models of the molds (isometric and 3 views) were created using SolidEdge. The machining was done at the machine shop in the mechanical engineering department.
Here is the base of one of our molds that I generated in SolidEdge.
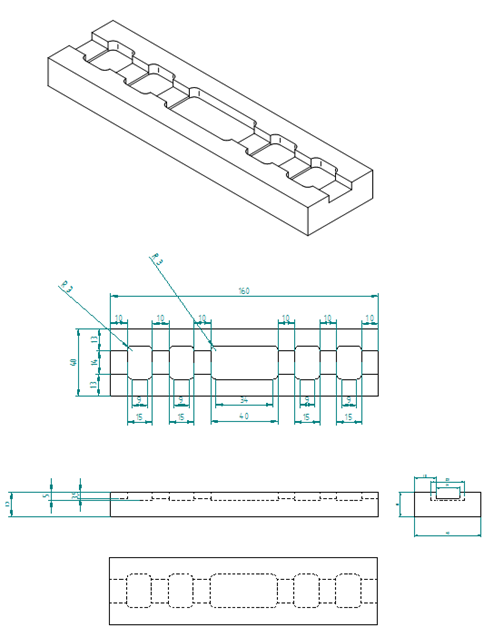
Here is the top cover of the same mold.
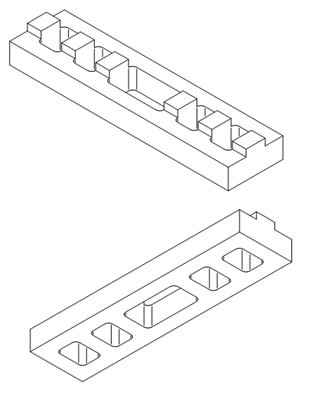
At the same time as I was working on the above ideas, another research strategy was considered. This second concept was to use thin sandwich bars or plates with a foam core layer between them. The outer plates can be made of a hard but flexible material. The foam core on the other hand would be soft enough to allow bending while at the same time offering resistance to it beyond a certain deflection. The foam would be coated with a polymer that changed its overall mechanical properties.
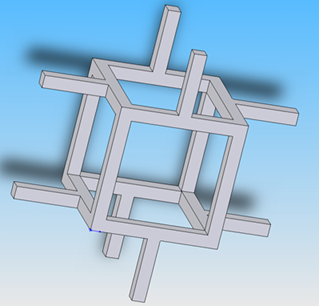
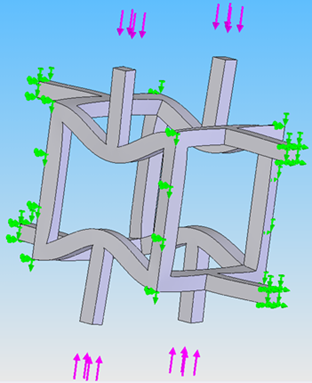
It was decided that it would be necessary to create foam models that can be used for computational studies. The starting point was the Gibson and Ashby cell foam model. This established model uses beams to represent foam cells, and standard beam theory to provide analytical results. The model was verified using SolidWorks for the CAD and CosmosWorks (now SolidWorks Simulation) for the FEA.
A foam cell according to the Gibson and Ashby model, as modeled by me in SolidWorks.
Loads were applied and different types of boundary conditions were experimented with to approximate the theoretical model results.
Foam samples were studied using an electron microscope. Numerous photos were taken of the different types of foams used in the research.

The images obtained from the optical microscope were processed using Image Pro and Adobe Photoshop.
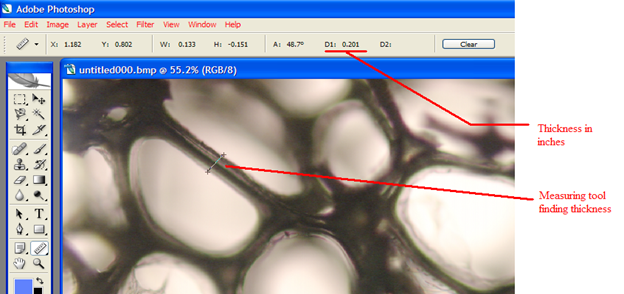
Here you can see photoshop being used to measure the width of the foam cell walls. These same dimensions could then be used in the finite element models. Tests were also carried out using an instron machine to obtain the mechanical properties of the foams.
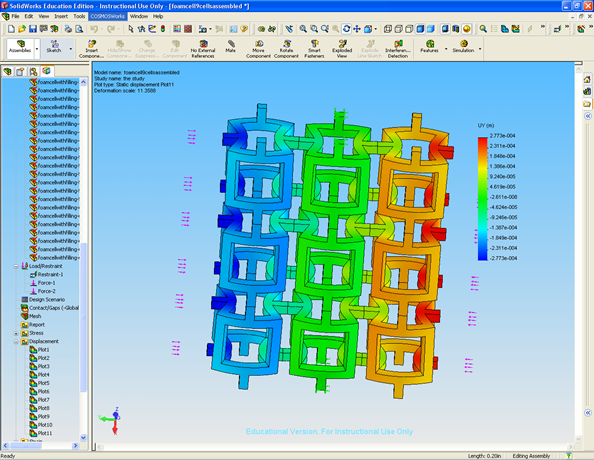
Finite element studies were then conducted on a network of these foam cells to find the correlation between the FEM models and experimental observations.
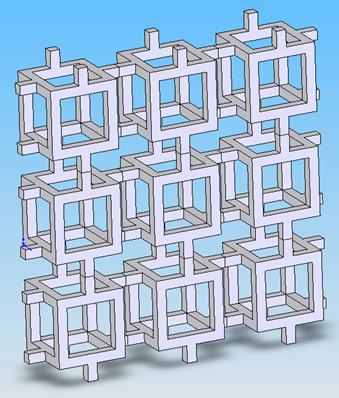
The foams were then coated with a polymer PEO. A correlation was found between the thickness of the PEO coating and the percentage of PEO in the solution. Here you see a foam cell coated after immersion in a 25% PEO solution.

Here you see new models of the coated foam cells.


These finite element models were used to develop relations for use in more complex foam structures.These relations indicated how a change in the modulus of the coating layer would affect the properties of the foam. It was theorized that if we used a polymer susciptable to temperature variations we could control the properties of the foam by changing the temperature.
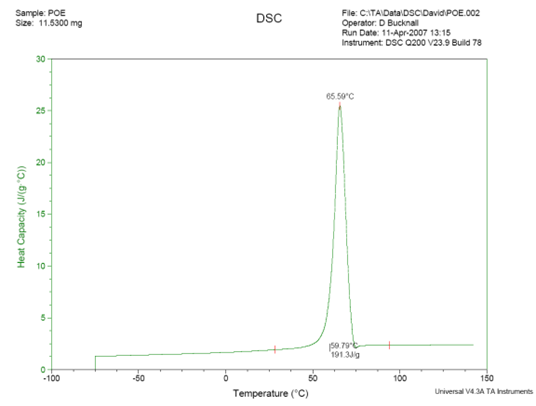
A differential scanning calorimeter was used to find the glass transition temperature of our polymer coating for further experimental studies.